Metrics for Regression Problems

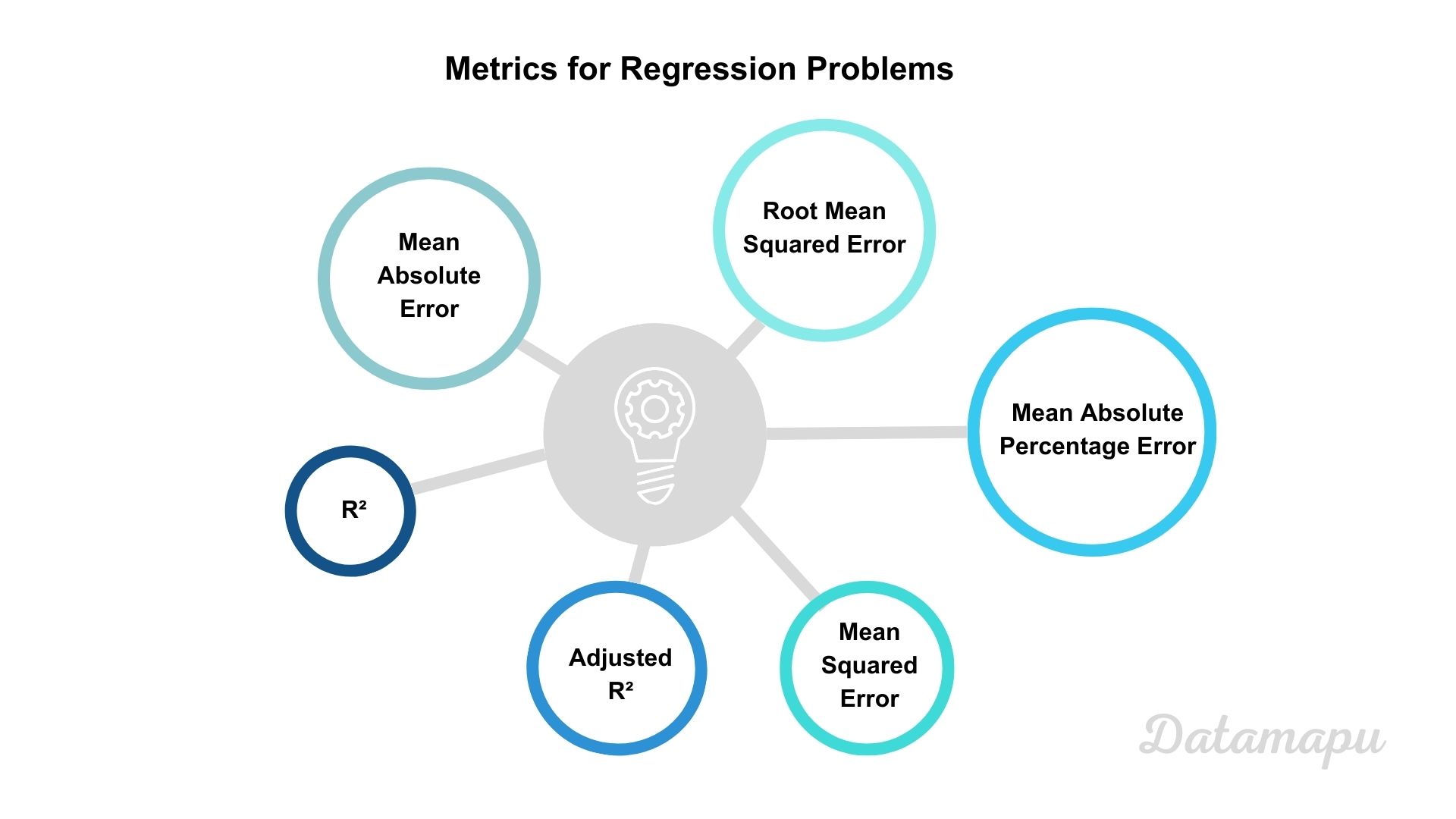
Regression Problems

Regression problems in Machine Learning are a type of supervised learning problem, where a continuous numerical variable is predicted, such as, for example, the age of a person or the price of a product. A special type is the Linear Regression, where a linear relationship between two (Simple Linear Regression or more (Multiple Linear Regression) is analyzed. The example plots in this article will be illustrated with a simple linear regression. However the metrics introduced here are common metrics for all types of regression problems, including multiple linear regression and non-linear regression. The simple linear regression is only chosen for illustration purposes.

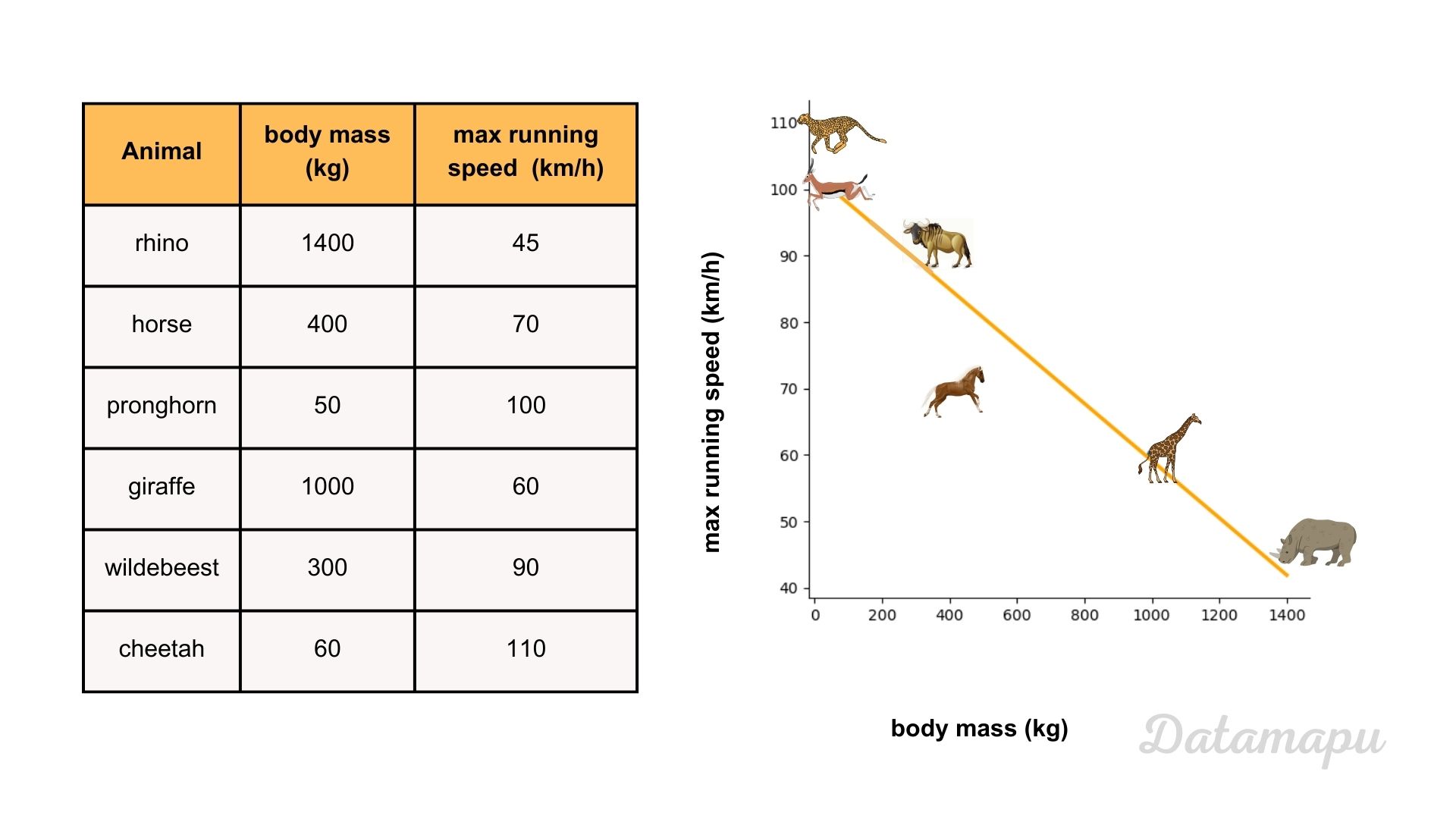Illustration of a simple linear regression between the body mass and the maximal running speed of an animal.

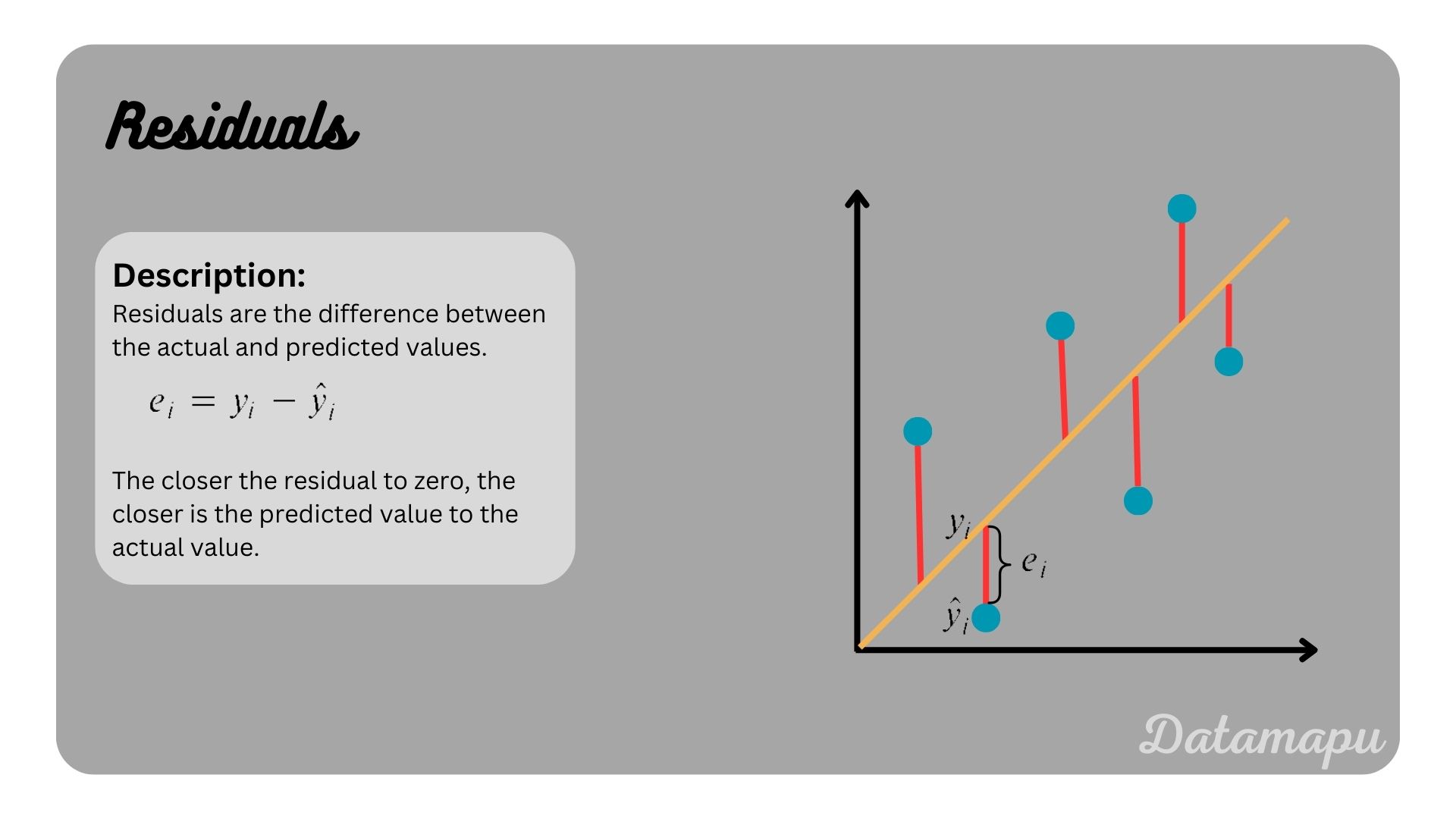
Residuals

In regression problems, the predicted results are rarely exactly the same as the true values, but lie either a bit above or below them. The difference between true and predicted values are a measure of goodness for the prediction and are defined as residuals. Metrics for regression problems are usually based on residuals.

Metrics

With the just defined concept of residuals, we can define different metrics that are useful for different error measurements.

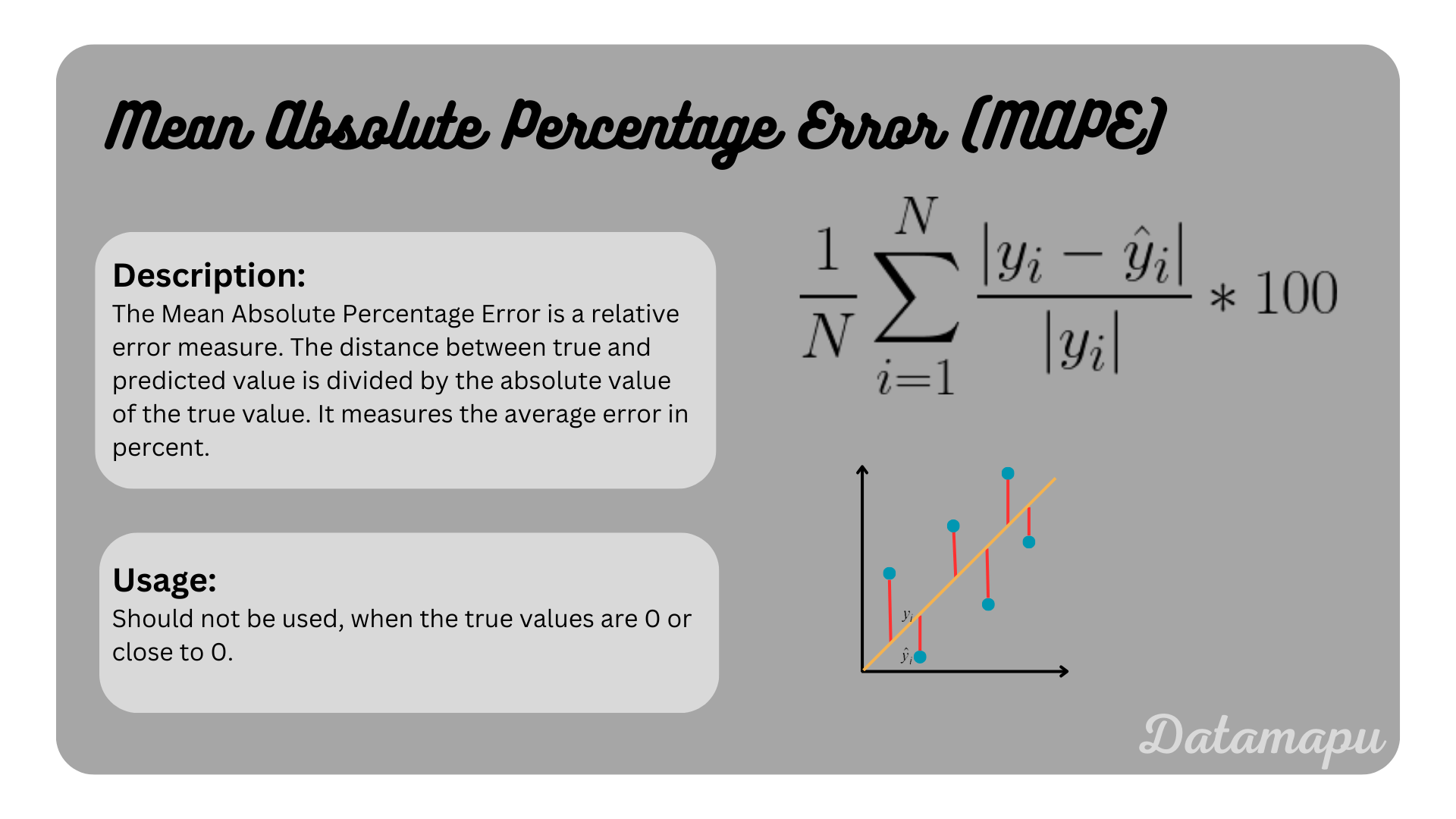
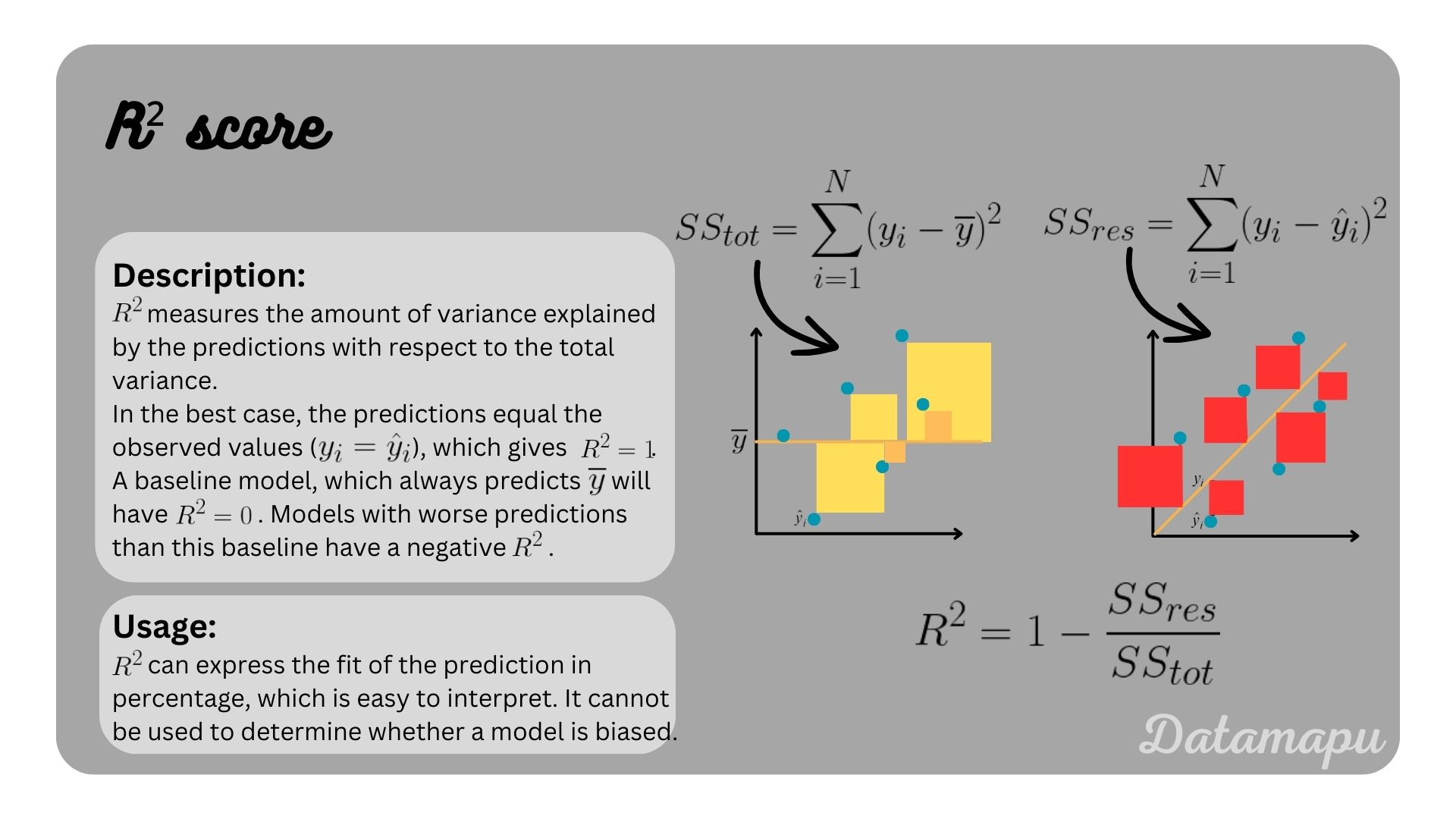
Example

Let’s consider the above example, relating the body mass of an animal with the maximal running speed, and calculate the RMSE. In order to do that, we first need to calculate the predictions. We use the LinearRegression method from sklearn to fit a linear regression and print the predictions.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

from sklearn.linear_model import LinearRegression

d = {'animal': ['horse', 'black rhino', 'giraffe', 'pronghorn', 'cheetah', 'wildebeest'], 
     'body_mass': [400, 1400, 1000, 50, 60, 300], 'max_speed': [70, 45, 60, 100, 110,  90]}
df = pd.DataFrame(data=d)

x = df['body_mass'].values.reshape(-1,1) 
y_true = df['max_speed'].values.reshape(-1,1)
reg = LinearRegression()
reg.fit(x, y_true)
y_pred = reg.predict(x)

This results is the following predictions (rounded to three decimals).

1

y_pred = [100.047 ,  99.617,  89.284,  84.979, 59.147,  41.926]

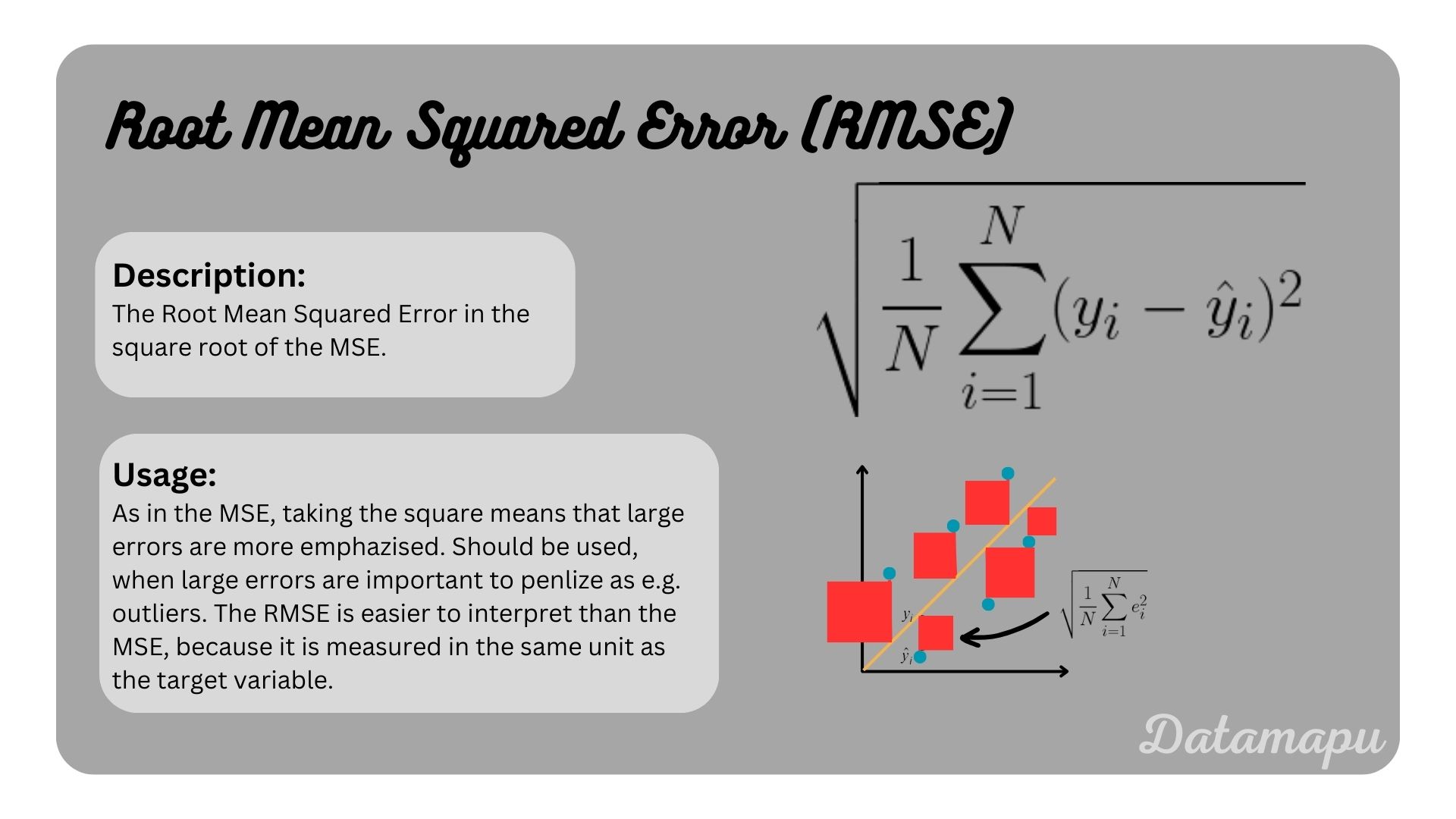
Using the formula from the previous section to calculate the RMSE, we get (rounded to three decimal).

In Python we can define our custom function to calculate the rmse.

1
2
3
4

import numpy as np

def rmse(y_true, y_pred):
   return np.sqrt(np.sum((y_true - y_pred)**2)/(y_true.shape[0]))

Alternatively, we can also use sklearn to calulate the RMSE.

1
2
3

from sklearn.metrics import mean_squared_error

mean_squared_error(y_true, y_pred, squared=False)

Both giving the same result 7.559 km/h as we calculated by hand.

Note, if squared=True in the mean_squared_error method, the MSE is calculated instead of the RMSE.

Summary

In this article we learned about the most often used metrics to measure the performance of regression problems and when to use them. They can be used for linear and non-linear regression and are generally based of the Residual Error between the true and the predicted value.

If this blog is useful for you, please consider supporting.

• Data Science
• Machine Learning
• Regression
• Metrics