Understanding Principal Component Analysis (PCA)

October 9, 2024 - 8 minutes read - 1589 words

Introduction

Principal Component Analysis (PCA) is an unsupervised Machine Learning algorithm for dimensionality reduction. In Data Science and Machine Learning, large datasets with numerous features are often analyzed. PCA simplifies these complex datasets by retaining their essential information while reducing their dimensionality. It transforms a large set of correlated variables into a smaller set of uncorrelated variables known as principal components. These principal components capture the maximum variance in the data. They are ordered in decreasing order of explaining variance. This makes it easier to identify patterns, reduce noise, and enhance the efficiency of Machine Learning models.

Why Use PCA?

When a dataset contains a large number of features, PCA can be a valuable tool for reducing its dimensionality. This dimensionality reduction simplifies the dataset while preserving most of the essential information. This approach can be beneficial for several reasons:

Avoid overfitting: High-dimensional data can lead to overfitting in Machine Learning models. Reducing the dimensionality may help to avoid the curse of dimensionality
Remove noise: PCA identifies and eliminates features that contribute little to the overall variance in the data and therefore removes redundant features.
Visualization: High-dimensional data can be difficult to visualize. PCA allows to reduce the dimensions to two or three, enabling clear visual representations that help in identifying patterns, clusters, or outliers.
Generate new features: PCA generates new features (the principal components) that are linear combinations of the original features. These components can be used as inputs for Machine Learning models.
Data compression: For large datasets, PCA can be beneficial to compress data by reducing the number of dimensions. This lowers storage needs, computational power, and time to process the data without significant loss of information.
Handling multicollinearity: When features are highly correlated, it can cause issues in regression models (e.g., multicollinearity). PCA transforms the correlated features into a set of uncorrelated principal components.

Conceptional Ideas

PCA makes use of several concepts of Linear Algebra, especially the fact that we can think of the dataset as a matrix. If we consider tabular data we can think of the features as the columns and the number of samples as the rows of the matrix. If we consider images we can think of the pixels as the entries of the matrix. PCA uses matrix transformation to rotate the original coordinate system of the features such that the new coordinates (the new features) are sorted by the amount of variance they represent in the data. To determine these new coordinates the Eigenvectors and Eigenvalues of the covariance matrix are calculated. The Eigenvectors sorted by the Eigenvalues in descending order represent the new coordinate system. Choosing the most important Eigenvectors permits the reduction of the dimensionality while keeping the largest amount of variance possible.

How Does PCA Work? - The Algorithm

The following steps describe how to achieve the transformed dataset.

1. Standardize the Data

Standardization ensures that each variable contributes equally to the analysis. If the variables have large differences in their ranges, the variables with larger scales could dominate the principal components. Standardization makes sure that all variables have the same contribution.

To standardize the data, for each variable the mean is subtracted and divided is by the standard deviation so that each feature has a mean of 0 and a standard deviation of 1. Mathematically this is formalated as

$$Z = \frac{X−\mu}{\sigma},$$

where $X = (x_1, \dots, x_n)$ is the original variable, $\mu$ is the mean, and $\sigma$ is the standard deviation.

2. Compute the Covariance Matrix

The covariance matrix captures how features vary together, which is essential for identifying the directions in which the data varies the most.

The covariance matrix for the centered dataset $Z$ is calculated as follows:

$$C = \frac{1}{n}Z^TZ,$$

where $C$ is the covariance matrix, $Z$ is the standardized data, and $n$ is the number of observations.

3. Compute and sort the Eigenvalues and Eigenvectors of the covariance matrix

Next, the Eigenvalues and Eigenvalues of the covariance matrix are calculated. This is also called Eigenvector decomposition. Every square matrix, and for that the covariance matrix can be written as

$$C = V \Lambda V^{-1},$$

with $V$ the matrix consising of the Eigenvectors as columns and $\Lambda$ a diagonal matrix of the Eigenvalues. The Eigenvectors determine the directions of the principal components, and the Eigenvalues determine their magnitude (importance).

4. Sort the Eigenvalues

The first Eigenvector, which is the one with the largest Eigenvalue, points in the direction of the highest variance, the second in the direction of the second large variance, and so on. That is, if we sort the Eigenvectors according to the magnitude in descending order we get the new feature space sorted by the magnitude of the Eigenvalues, and we get the new feature space ordered by the magnitude of the variance. Each Eigenvector represents a feature in the new feature space and since the Eigenvectors are orthogonal, the new features are uncorrelated.

5. Select the Principal Components

We can use the Eigenvectors from the covariance matrix to rotate the coordinate system of the feature space. When using all eigenvectors we keep all the information, but the dimension of the new coordinate system is the same as of the original one. To reduce the dimensionality, we need to reduce the number of Eigenvalues and Eigenvectors. Since we sorted the Eigenvalues by their magnitude, we can choose the top $k$ Eigenvectors and get a dataset that represents the maximum amount of the explained variance in the data. The exact number $k$ we choose depends on the amount of variance of the data to be present in the data. The sum of the top $k$ eigenvalues divided by the sum of all eigenvalues gives the proportion of variance explained by the selected components.

6. Transform the Data

To represent the original data in the new lower-dimensional space, we multiply the standardized data by the matrix of the selected eigenvectors. This projects the original data onto the new feature space defined by the principal components. Mathematically, this can be formulated as

$$Z_{new} = Z W,$$

where $Z$ is the standardized data, and $W$ is the matrix of the selected eigenvectors.

Explanations

Let’s try to better understand why the eigenvectors of the covariance matrix can be used to transform the data to preserve the highest amount of variance. First, consider the meaning of the covariance matrix. The covariance matrix contains information about the variances and covariances of the data. It determines how much the data spread in each direction. The variance along a specific direction can be determined by projecting the covariance matrix onto the vector corresponding to that direction. This projection is defined by the scalar product of the covariance matrix and the vector, which can be written as $v^T C v$, where $C$ is the covariance matrix and v is the vector.

If $v$ is an eigenvector, $v^T C v$ represents the variance in the direction of the eigenvector $v$. If $\lambda$ is the corresponding eigenvalue of $v$, the equation $C v = \lambda v$ holds. When $\lambda$ is the largest eigenvalue, the expression $v^T C v$ is maximized, meaning the direction of $v$ (the eigenvector) corresponds to the direction of the greatest variance in the data. Thus, the eigenvector associated with the largest eigenvalue indicates the direction in which the data has the most spread (variance).

2d-example for the rotation of the coordinate system in the direction of the highest variance.

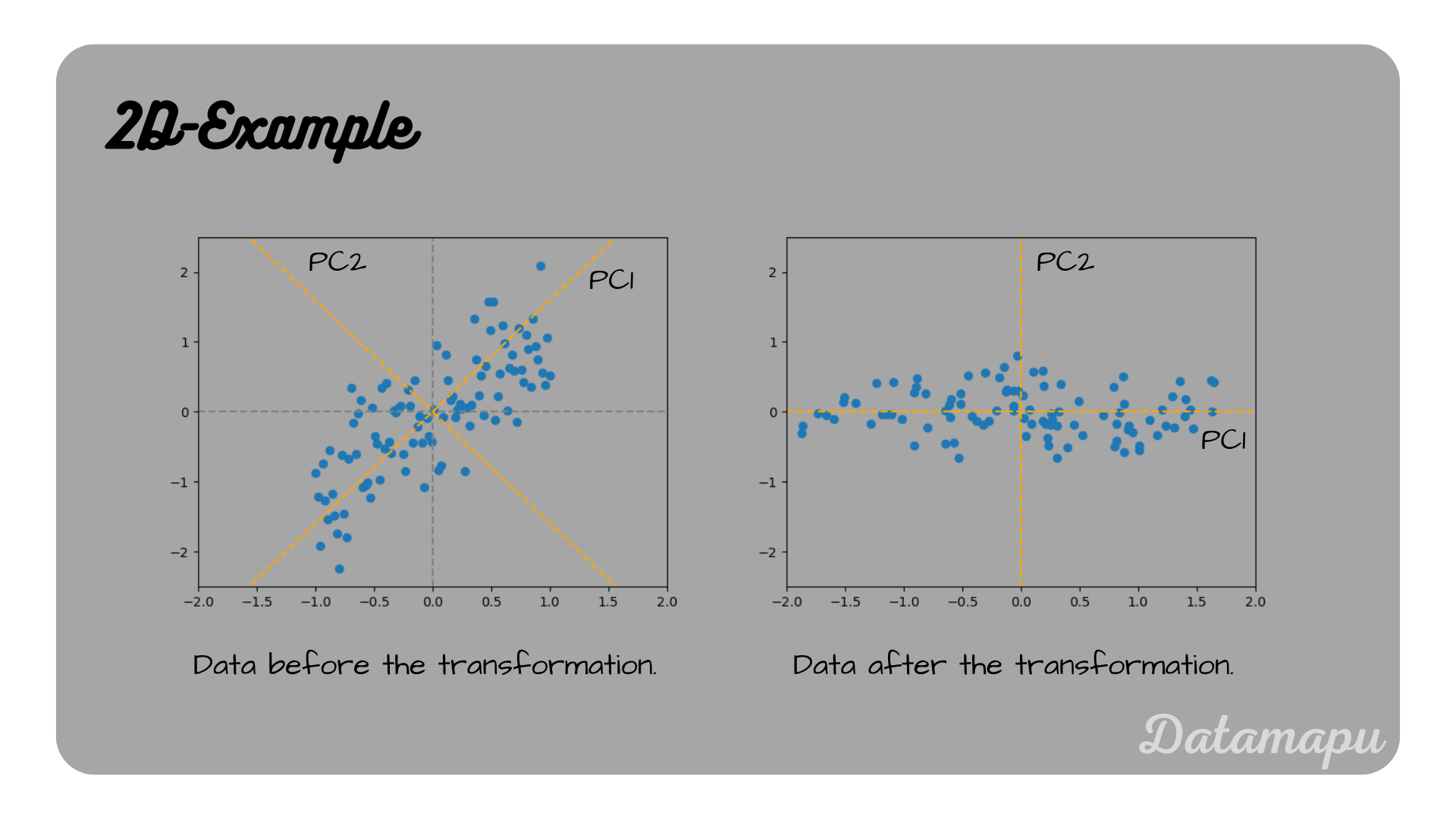PCA Example for 2 features.

PCA in Python

To perform a PCA with Python we can use the scikit-learn package. The method PCA, lets us define the number of components, we want to keep. This number must be smaller or equal to the number of features. The data can be given as a pandas data frame or a numpy array. The above plotted example, can be calculated as follows. Assume the data is stored in a data frame df.

1
2
3
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
components = pca.fit_transform(df)

After calculating the PCs, we can access the explained variances, the singular values (eigenvalues) and the new features (rotated coordinates).

1
2
3
print(pca.explained_variance_ratio_)
print(pca.singular_values_)
print(pca.components_)

In the above case we are considering an example of only two features, that is using 2 principal components rotates the coordinate system into the direction of the highest variance, but it does not reduce the dimensionality. In general, a PCA would be used, when the feature space is large and n_components would be chosen smaller than the number of original features.

Summary

A PCA is used to reduce the dimensionality and with that the complexity of the data. This dimensionality reduction is done by projecting the data onto the components that reflect the highest amount of variance, which are the eigenvectors of the covariance matrix. Only the components maintaining a certain amount of the variance - which we need to define - are kept and the rest is neglected. The principal components are orthogonal and therefore uncorrelated. PCA can help to identify patterns in the data.

Appendix

Eigenvector: A non-zero vector that, when multiplied by a matrix, only changes in magnitude (not direction). Mathematically, for a matrix $A$ and eigenvector $𝑣$:

$$A 𝑣= \lambda v,$$

where $\lambda$ is the eigenvalue corresponding to that eigenvector $v$.

Eigenvalue: A scalar that indicates how much the eigenvector is stretched or compressed when multiplied by the matrix.

Covariance Matrix:

The covariance matrix of a random vector $X = (X_1, X_2, \dots, X_n)$, with $n$ random variables $(X_1, X_2, \dots, X_n)$ has the following form

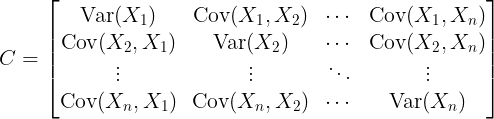
covariance

If this blog is useful for you, please consider supporting.